|
Астронет: С. Б. Попов, М. Е. Прохоров Классифицированные обзоры 2-й версии за 2003 г. (04/2003 - 12/2003) - ... The R.A.P. Project (Reviews of Astro-Ph) http://www.astronet.ru/db/msg/eid/rap-them2003 /dynamics.html |
Динамика, механика и т.п.
(Архив Динамика: v.2, 2004,
v.1, 2002-2003)
Authors: P.Goldreich, N.Rappaport
Comments: 16 pages, 7 fig.
Прометей и Пандора - два спутника-"пастуха", движущихся по краям самого внешнего из колец Сатурна. Их периоды обращения достаточно близки: средние движения этих двух спутников находятся в резонансе 121:118. Авторы численно исследовали возможность проявления хаоса в данной системе, обнаружили, что хаотическое движение возникает, и смогли понять его причину (дифференциальная прецессия расщепляет основной резонанс на четыре узкие, близко расположенные, равноотстоящие по частоте компоненты, либрация уширяет их до сильного взаимного перекрытия, в результате чего образуется зона хаотических движений). Хаос в этой системе проявляется в том, что положение спутников на их орбитах может отличаться от предсказываемого средним движением для Прометея на 1.8o/год, а для Пандоры - на 3.1o/год. Если бы массы спутников были в несколько раз меньше, их движение было бы регулярным.
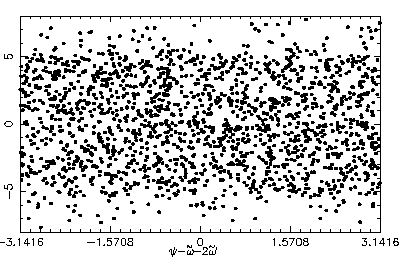
Иллюстрация хаотического движения в системе Прометей-Пандора: по горизонтали отложено положение одного из спутников на орбите, по вертикали - отличие разности орбитальных фаз спутников от ожидаемого при среднем движении.
Authors: James C. Lombardi et al.
Comments: 20 pages, submitted to MNRAS
В плотных ядрах шаровых скоплений наряду с близкими пролетами одиночных звезды начинают играть столкновения одиночных звезд с двойными системами и взаимные столкновения двойных систем. Такие столкновения могут приводить не только к образования сливающихся двойных систем, но и к системам в которых происходит последовательное попарное слияние трех или даже четырех звезд. Образовавшиеся подобным путем звезды могут иметь существенные химические и эволюционные особенности. Образование подобных систем и процессы слияния в них являются основной темой данной статьи и рассмотрены достаточно подробно.
Authors: N.Rambaux, E.Bois
Comments: 15 pages, 14 figures, 3 tables, submitted to A&A
До 1965 года считалось, что Меркурий обращается вокруг Солнца синхронно (подобно Луне вокруг Земли, орбитальный и осевой периоды при этом равны). В 1965 году было показано, что это не так, Меркурий обращается вокруг Солнца в спин-орбитальном резонансе 3:2 (осевой период - 58.656 дня, орбитальный - 87.969 дня). Этот неожиданный резонанс связан с ненулевым эксцентриситетом орбиты Меркурия и существенной асимметрией самой планеты. Данные, полученные космическими аппаратами MESSENGER и BepiColombo, позволили построить новую более точную теорию движения Меркурия. Эта теория позволяет предсказать его либрации. В движении планеты выявлены два собственных периода (15.847 и 1066 лет) и вековой резонанс (на частоте 278898 лет).
Authors: S. I. Ipatov and J. C. Mather
Comments: International workshop "First Decadal Review of the Edgeworth-Kuiper Belt - Towards New Frontiers"
Проблема имеет вполне насущную важность - транс-нептуновые объекты пояса Койпера - самый большой резервуар астероидов и комет в Солнечной системе. Миграция даже малой их части к планетам земной группы может иметь существенную астероидную опасность. Подобной миграции в первую очередь подвержены объекты на эллиптических орбитах, перигелии который близки к орбите Юпитера. Моделирование 13000 подобных объектов показало, что примерно 0.1% из них будут пересекать орбиту Земли.
Authors: Barrie W Jones, David R Underwood, P Nick Sleep
Comments: 6 pages, 2 Figures, Heidelberg Conference titled "The Search for Other Earths"
Сейчас известно уже около 100 планетных систем. Но все это планеты-гиганты. Стоит ли искать планеты земного типа именно в этих системах? Находятся ли такие планеты в условиях, когда в принципе возможна жизнь земного типа? Авторы статьи рассчитали устойчивость орбит типа Земли для девяти известных систем и показали, что в большинстве случаев они являются устойчивыми для расстояний, соответствующих благоприятным для жизни условиям. Экстраполяция на все 93 системы вокруг звезд главной последовательности, известные на данный момент, дает такой результат: примерно в трети случаев можно ожидать наличие устойчивых орбит в "обитабельных" зонах.
О будущих поисках планет земного типа с помощью коронографов см. небольшой (8 страниц) обзор "Terrestrial Planet Finding with a Visible Light Coronagraph".
Authors: D. Pooley et al.
Comments: 11 pages, 1 b&w figure, 1 color figure
Уже давно ученые понимали, что маломассивные рентгеновские двойные очень эффективно рождаются в шаровых скоплениях . Однако, всегда нужны как можно более прямые наблюдательные подтверждения любой подмеченной закономерности (какой бы очевидной и естественной она не казалась). В этой статье авторы дают прямые наблюдательные указания на то, что количество тесных двойных в шаровых скоплениях тесно связано с числом тесных сближений звезд. Разумеется, авторы дают оценку полного числа маломассивных двойных в шаровых скоплениях нашей Галактики.
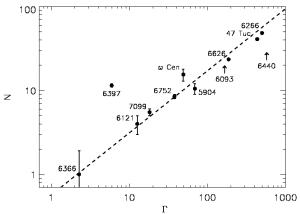
Используются данные Чандры по 12 скоплениям. Этот спутник может видеть даже очень слабые источники, поэтому статистика выделения числа рентгеновских двойных очень хорошая. Далее, по известному соотношению, зная плотность звезд и их распределение по скоростям, можно определить чсатоту тесных сближений звезд скопления. Теперь остается построить график, где по одной оси отложено количество рентгеновских источников (N), а по другой - частота сближений (Г).
Authors: Eva-Marie David et al.
Comments: Accepted for publication to PASP, 26 pages including 9 figures
Достаточно реалистичные численные расчеты поведения планет типа Земли
(имеется ввиду масса) в двойных системах. Не вдаваясь в детали:
около половины всех двойных допускают существование устойчивых орбит
на протяжении как минимум 4.6 миллиардов лет.
Authors: L. Velazquez (Universidad de Pinar del Rio, Cuba) and F. Guzman (Instituto Superior de Ciencias y Tecnolog\'ia Nucleares, Cuba)
Commets: 7 pages, 2 eps figures Subj-class: Statistical Mechanics
У самогравитирующих систем нет положения равновесия с минимальной возможной энергией, следовательно, к ним нельзя применять обычный термодинамический подход. А очень хочется. Что делать? Авторы этой (и следующей cond-mat/0303492) статьи считают, что переход к термодинамическому пределу возможен. Для этого надо устремить число частиц N в системе к бесконечности сохраняя величины E/N7/3 и EN1/3 постоянными (здесь E - энергия системы, а L - ее угловой момент).